Reinforcement Learning as Probabilistic Modelling: A Variational Inference Formulation (Part II) WIP

Having introduced the variational inference formulation of dynamical systems, now we are ready to formulate reinforcement learning as a special-case of latent-variable models. We show how to derive this formulation from first principles, and present a couple of important special cases. If you are familiar with variational inference, please go ahead and read this post. If not, you might be interested in skimming over Part I for a refresher.

There are numerous posts on reinforcement learning and amazing lectures, such as these delivered by David Silver. This post is not meant as a repetition but rather attempts to provide an alternative view, which can be seen as a generalisation of the current framework.

Typical definitions of reinforcement learning take the Markov Decision Process as a starting point. Here, an agent interacts with an unknown and uncertain environment with the goal of acquiring an optimal behavioural policy (or action-selection rule) that maximises total expected return. From there, a (stochastic) optimisation problem is defined and multitude of algorithms are proposed to acquire an "acceptable" policy. These algorithms typically interact with the environment gathering experience in form of trajectories that are then used to update the policy.

We seek an alternative view to the whole control problem by starting from probabilistic modelling. We develop our definitions and then relate-back to current literature on reinforcement learning. Hopefully, seeing the reinforcement learning problem from a different perspective gives the reader a fresh view on reasoning about such types of problems.

Before diving into the latent variable model definition of reinforcement learning, let us present the standard formulation from Markov decision processes. Here's a description from one of my papers:

The definition above simply states the main constituents of a reinforcement learning problem, and describes the process by which an agent interacts and evolves in an unknown environment. Next, we describe the probabilistic modelling perspective on reinforcement learning as a specific form of latent variable models.

Reinforcement Learning as a Latent Variable Model:

To reason about reinforcement learning within the context of latent variable models, we need to introduce two variables, observables and latents. Have a look at this for a refresher.

We assume that the observed variable corresponds to a binary reward event, while the latent corresponds to a trajectory. Of course, the notion of a binary reward is less common in standard reinforcement learning frameworks. However, it is "relatively" easy to transform total rewards to a binary event as we detail later.

I like to think of these choices as intuitive. Let me illustrate!

In the previous post, we described latent variables as these affecting (or generating) our observables, e.g., a hidden dynamical model that generates the observed joint values of a robot. Similarly, the driving generator of the binary reward event is a trajectory. Depending on how favourable (in terms of total accumulated reward) is a trajectory, we either observe a binary event of 0 or 1. Similar to classic latent variable models, we condition the binary reward event (observable) on the trajectory random variable (latent). These assumptions are depicted in the graphical model below. Keep in mind that the trajectory is a resultant of an agent interacting with the environment, and as such is a sequence of state-action pairs.

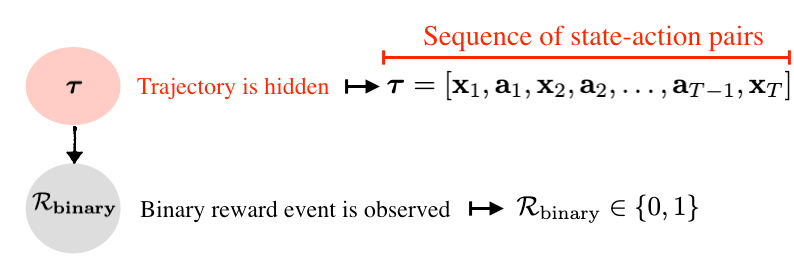
In the standard setting of latent variable models, we parameterised the distribution between the latent and observable variables by, for example, adding a zero-mean Gaussian noise to the output of an unknown parameterised function. We might be tempted to go along the same direction to compute the value of the binary. Though interesting, our problem is relatively simpler as one can easily determine the value of the binary event dependent on the value of total rewards. There are multiple ways this conversion can be done. Have a look at this awesome survey by Marc, Gerhard, and Jan (pp. 44) for more details concerning this step.

BTW, I really believe that a lot of the work in RL nowadays relates to that done by Jan and his team -- I mean the idea of KL constraints for natural gradients in RL has been there since 2005, have a look at NAC and attempt to relate to current algorithms (e.g., TRPO, KFAC). Interesting!

We follow one such conversion, and assume that the binary reward event is exponentially distributed given some trajectory. We also introduce a tuneable (temperature) parameter that allows for reward scaling:

---

Cool! So, we have our graphical model, we have the distribution relating latents to observables. What's next. Well, let us try to understand what is it we want to maximise. In other words, let us attempt deriving the optimisation problem similar to what we did in Part I.

Back in the standard setting, we wanted to maximise the marginal distribution of our observations. To do that, we introduced the latent variables using marginalisation and commenced to derive the evidence lower-bound that gave us the optimisation problem. One thing to keep in mind though is that in reinforcement learning we are only interested in a part of these observations. Specifically, we would like to maximise the distribution of "good" trajectories, i.e., these that correspond to a binary-event of 1. Alright then, let's proceed in a similar fashion!

The figure below presents the initial steps in constructing the optimisation problem. We follow similar steps to these in Part I. Namely, from the marginal over the binary reward event (observed variable), we introduce latents using marginalisation. We then incorporate the logarithm that simplifies the problem and allows the usage of Jensen's inequality.

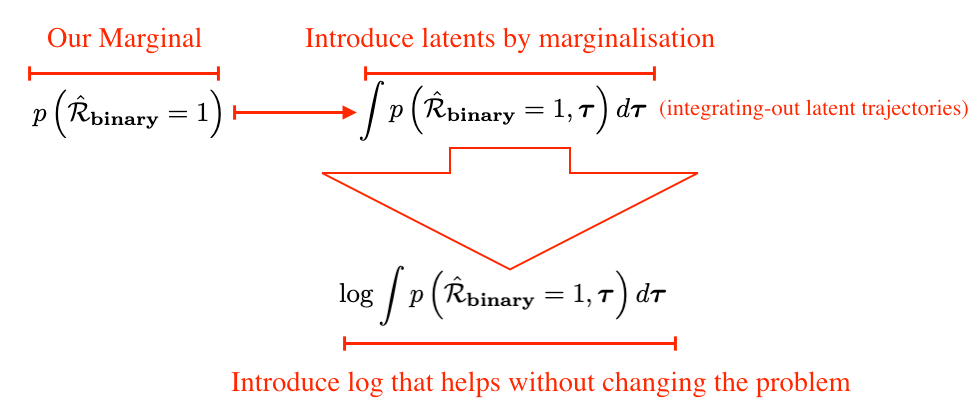
Now, we introduce the distribution of binary rewards conditioned on trajectories (the one defined above) by simply applying Bayes rule:

Interestingly, the equation in the previous figure is closer and closer to the optimisation problem familiar to reinforcement learning practitioners. For instance, the first term under the integral already contains a transformation of the total-expected return, which we typically maximise in reinforcement learning. The second represents the density of a trajectory following a policy. When combined with the integral this is just an expectation under the trajectory distribution. In short, this equation is similar to denoting the expected (transformed) rewards.

Having defined the first term under the integration sign, we now attempt to understand the density of a trajectory following some policy. This distribution is not specific to the variational inference formulation of reinforcement learning, and easily accessible from standard literature. Even so, let us derive it to fully understand the implications. As defined earlier, a trajectory is just a sequence of state-action pairs, collected by an agent after starting at some initial state and following some policy thereof. Consequently, the density of a trajectory is nothing but the joint density over these state-action pairs, which we can factor (using the chain rule) in terms of the Markov decision process components, such as the transition model, and the policy.

---

The first step of the chain rule application is shown the figure above. Again, we have two steps. In the first, we condition on other variables, and in the second we multiply by the joint of the remaining variables. Of course, this process has then to be recursed to the initial state.

Great! Before moving forward with our derivations, let us take a moment to try to understand the conditional we attained in the first step of the above derivation. Since we operate in a Markov decision process, we know that the state at the last time step only depends on the state and action at the previous time-step and not on all the path's history. Clearly, this is nothing but a transition density of the MDP!

Now, let us repeat these factorisation steps for the second term. We get:

This looks like a messy set of equations, but it is really easy to understand. In Step 2, we had a joint distribution over state-action pairs from time T-1 to 1. We apply the chain rule for factorising densities again. In the first step, we condition the last variable on others, while in the second we multiply by the joint of the remaining variables, and then we repeat. If we inspect the term in Step 2.1 carefully, we come to realise this is nothing but the density of an action conditioned on a state and a lot of other things. We know from the definition of our policy, however, that our action only depends on the state. Thus, we can ignore all the other terms beyond T-1 and arrive at nothing but the policy.

It is worth noting that if we were to consider the partially observable case (e.g., POMDP), we would have not been able to get rid of the history making the problem harder. We leave the discussion of POMDPs for future posts.

Applying this factorisation back to the initial time-step, you should now be able to convince yourself that the density of a trajectory can be written as:

The Reinforcement Learning Evidence Lower Bound (RL-ELBO):

We recognise that our optimisation problem requires a marginalisation over trajectories. Unfortunately, computing this integral is difficult due to a variety of reasons. Among other problems, if we are to compute the integral in closed-form, we require particular knowledge of the state transition dynamics, which is typically unavailable in reinforcement learning. To make matters worse, even if we were to know our stochastic transition model, conjugacy with the policy density is necessary for a closed-form solution; an assumption that can become too restrictive for complex dynamical systems. Not only the transition and policy models lead to difficulties in computing

the integral, but so does the normalising term of the reward distribution, especially when the reward function is unknown upfront (e.g., model-free reinforcement learning).

To remedy the problems above, we will borrow ideas from variational inference, which, as discussed in the first, turns inference into optimisation by introducing a variational distribution over the latent variables -- the trajectories.

The steps we are going to follow next are similar to what we have done in Part I, where we: 1) introduce a variational distribution, and 2) use the variational distribution to derive an upper-bound to the exact intractable optimisation problem. With this, we write:

To derive the RL-ELBO, we just apply Jensen's inequality after multiplying and dividing the marginalisation equation by the variational distribution. We then expand the logarithm and write the resulting equation in terms of a KL-divergence (a measure of similarity between probability densities) between the variational and the real distribution.

Maximising the RL-ELBO leads to the following general optimisation problem:

Hold on! The optimisation problem above is very similar to standard reinforcement learning. The first term includes expectation over total discounted reward (up to a constant), while the second can be simply seen as a regulariser. Using different choices for the variational and model distributions, we can derive a wide-range of reinforcement learning algorithms from this general problem formulation, as we detail next.

Choices of the Variational Distribution & Special Cases:

We have realised that the reinforcement learning problem can be written as a problem of maximising the RL-ELBO with respect to two densities, i.e., the variational and model policies. Now we show how some approaches from recent reinforcement learning literature can be derived as special cases of the framework above.

These approaches differ in their representation for the policy, the variational policy, and the way they optimise over them. Several recent reinforcement learning methods treat the policy as a given prior, and only consider update the variational one. Such a formulation is definitely inspired by variational inference literature that assumes a prior model on latent variables. Using this special-case, for example, we can recover maximum entropy reinforcement learning as we show later.

Other reinforcement learning algorithms optimise the RL-ELBO by using an alternating update scheme that switches between fixing the policy and optimising for the variational and then fixing the variational and optimising for the policy itself.

Working in such an alternating optimisation framework can be seen as the more general setting between the two as it assumes both the policy and the variational policy (or their parameters) as optimisation variables.

Several special cases of the general alternating-optimisation method exists that approximate or even drop one of the steps. In the what comes next, we discuss different instantiations of this general scheme.

Maximum-Entropy Reinforcement Learning:

Before deriving maximum entropy reinforcement learning, we note that this framework assumes a regularised reinforcement learning objective. Particularly, maximum entropy reinforcement learning maximises rewards, while introducing an entropy regularises that is used to guarantee non-collapsing policies.

Such a regularisation scheme is easily derived from the RL-ELBO by making assumptions on the policy and the variational distribution qπvariational. First, the policy is assumed to be given and not optimised for in the RL-ELBO. Particularly, the policy is assumed to be uniform. Moreover, the variational distribution structure is also assumed to abide by that of the model with the difference that actions are executed using a variational policy:

In other words, the variational distribution over trajectories does not alter the initial state distribution nor the transition dynamics.

We can relax these assumptions in model-based reinforcement learning. I will detail these in later posts.

With these assumptions, we can now simplify the RL-ELBO. Let's do so step-by-step. Commencing with the KL-term, we get:

Viola! We got our regulariser. The last term in the above equation is nothing but the conditional entropy of the variational policy that is used to reduce policies from collapsing.

Having handled the KL-regulariser, now we shift our attention to the first term of the RL-ELBO (i.e., the term resembling likelihood in standard variational inference):

Plugging everything back in the RL-ELBO, we attain:

Max-Entropy Reinforcement Learning Policy Gradients:

One way we can optimise for the variational distribution is by adopting a policy-gradient method that simply updates a parameterised policy by stochastic gradients. To do so, we parameterise our variational distribution by a set of unknown parameters and perform gradient ascent to fit their values. For example, if we think of the variational policy as a deep-neural network mapping from states to actions, the variational parameter would correspond to the weights (and biases) connecting its layers.

To make such a policy stochastic, we can apply a similar trick to that discussed in the previous part. Namely, we can perturb the output of the network with a multi-variate Gaussian noise and as such get:

For the discrete case, we can have the network output directly a soft-max distribution, which can also be fit. More details on this step can be found in the Sergey's cool survey as well.

Of course, no one cares for the gradients of the RL-ELBO given auto-diff and the awesome revolution of plug-and-play. Well, I do. I know this looks like black-magic, but let us derive (at least in part) these gradients.

---

Standard Policy Gradients:

To fully comprehend how these gradients can be derived, there are some ideas from policy gradients that are needed for exposure. Let's detail these first:

Likelihood Ratio Trick: When deriving policy gradients update we encounter a gradient of an expectation, where the distribution under which this expectation is taken is parameterised. To compute such a gradient we following these steps:

The last thing to remember is the derivation of the density of the trajectory that we've done before. With this, we can rewrite the gradient of the logarithm of that density as:

Variance Reduction:

Policy gradients are typically inefficient due to the large variance of the likelihood ratio estimator as described above. To have more sample efficient algorithms, a variety of variance reduction techniques have been introduced in reinforcement learning, e.g., subtracting a constant baseline, exploiting temporal structure, among others. I will dedicate a separate post for such techniques elaborating on the connection between baselines and control variates. Here, we briefly discuss two such techniques that can be used to reduce the variance of a likelihood ratio estimate.

Subtracting a Baseline:

One way to reduce variance of our gradient estimate is to subtract a baseline that is either constant or state-dependent without making gradients biased. Please note that if your baseline depends on both the states and actions the estimate is typically biased. Check this out for more information. There is a multitude of ways to choose your baseline ranging from averaged rewards, to ones that denote the expected return. Here's an example of some of the baseline typically used in reinforcement learning:

Exploiting the Temporal Structure:

Removing terms from the overall summation that do not depend on the current action generally reduces variance. In addition to subtracting a baseline, we can take advantage of this observation in our problem to further reduce the variance. Particularly, if the policy remains unchanged, we know that future actions are independent of past rewards. Hence, we can remove past rewards from the current estimate of the gradient to significantly reduce variance. Simply put, if we are at the current time-step, we can remove rewards received before as follows:

Please note that if we choose the baseline to be the state dependent one, we would end-up with what is known as the advantage-actor-critic framework. In this case our gradient estimate is written as:

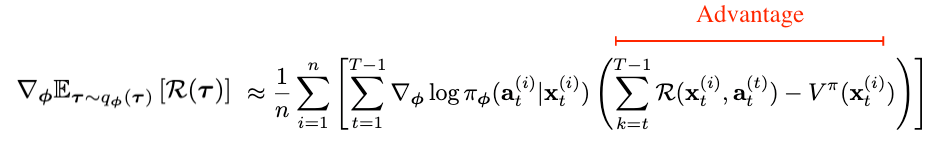
We won't dig deeper into actor-critic-type algorithms, but we briefly mention that generally there are two strategies used to estimate the value function. The first regresses against empirical returns, while the second used the Bellman optimality equations. Interested readers are referred to these awesome slides from Sergey for more details. Milica has also an amazing lecture on actor-critic methods that you can consult.

---

Applying these ideas to our derivations of maximum-entropy reinforcement learning, you should be able to easily attain the equations in Section 4.1 of Sergey's survey on probabilistic inference and reinforcement learning.

I would leave these derivations as an exercise to the reader. Please do not hesitate to contact me if you found difficulties attaining these forms.

Rather than directly optimising the RL-ELBO, we could have followed a message passing interface.

This would have led us to different forms that relate to soft-Q-learning-types of algorithms. The details of these steps are beyond the scope of this post. But now, you should be ready to tackle such derivations with more confidence.

Another common special case of the RL-ELBO is an algorithmic class referred to as Monte-Carlo Expectation-Maximisation (MC-EM) policy search. MC-EM optimises over the policy, while not introducing an explicit variational distribution. Instead these algorithms rely on a sample based approximation of the distribution over trajectories. We won't dive into these algorithms here, but readers can find more information in this nice article (pp. 41 onwards).

Cool! Now, you know how to mix variational inference with reinforcement learning. In the next post, I will detail how we can extend these topics to multi-task reinforcement learning. Stay posted!

This blog post would have never been possible without the help of others. Shout to:

Rasul Tutunov (Proofreading, and checking the maths)

Lots of other papers and posts (Links in the main text)

If you found this post useful in your research please cite as:

Bou Ammar, H., Tutunov, R., Reinforcement Learning as Probabilistic Modelling: A Variational Inference Formulation (Part II), Blog 2019.

[i don't own any of the pictures (including cover) in this post]